Lukuseulan normit
Lukuseulan normiarvot on laskettu suomen kieli ja kirjallisuus -oppimäärää (S1) opiskelevien tulosten perusteella. Aineisto kerättiin vuosina 2021–2023. Ennen normiarvojen laskemista, aineistosta poistettiin suomi toisena kielenä ja kirjallisuus -oppimäärää (S2) opiskelevat oppilaat. S2-ryhmään kuuluvat jätettiin normien ulkopuolelle, koska emme tienneet, liittyivätkö lukemisen vaikeuksia indikoivat tulokset suomen kielen taidon heikkoon tasoon vai lukutaidon pulmiin.
Lukuseulan testit on normitettu syksylle ja keväälle kaikilla muilla vuosiluokilla paitsi ensimmäisellä. Ensimmäisen luokan osalta normit on laskettu vain keväälle, koska valtaosa koulutulokkaista ei osaa vielä lukea. Lerkkasen ja kumppaneiden (2004) mukaan noin puolet suomalaisista koulutulokkaista osaa nimetä kaikki kirjaimet ja noin neljännes pystyy lukemaan sanoja sujuvasti.
Testeistä saadut tulokset vertautuvat automaattisesti sen ajankohdan normeihin, jolloin testi teetetään. Jos testi teetetään syksyllä, tuloksia verrataan syksyn normeihin. Keväällä teetettyjä testejä verrataan kevään normeihin. Testi tuleekin teettää koko ryhmälle joko syksyllä tai keväällä. Jos testi teetetään osalle ryhmästä syksyllä ja osalle keväällä, kaikkien ryhmän oppilaiden tuloksia verrataan syksyn normeihin.
Miten tulokset esitetään ja lasketaan?
Tulokset esitetään Lukuseulassa keskimääräisinä ratkaisuprosentteina (0–100 % oikein). Keskimääräinen ratkaisuprosentti lasketaan jakamalla saatu pistemäärä tehtävän maksimipistemäärällä. Esimerkiksi epäsanatehtävän maksimipistemäärä on 30 toisella luokalla. Jos arvioitava saa tehtävästä 15 pistettä, ratkaisprosentti on 50 %. Arvioitava voisi saada teknisen lukutaidon tehtäväpaketista syksyllä oikein seuraavat osuudet: epäsana, 50 %; kirjoitusvirhe 30 %, sanajono, 20 %, tavutus, 90 %. Teknisen lukutaidon kokonaistulos laskettaisiin tässä tapauksessa seuraavan kaavan mukaan: (50 + 30 +20 + 90) / 4 = 47,5 %. Teknisen lukutaidon ratkaisuprosentti (47,5) näkyisi tulospalvelussa harmaana pylväänä eli tulos sijoittuisi jakaumassa 50–80 prosenttiin (ks. 2. luokan syksyn normit) eli tulos sijoittuisi Lisätietoa tulosten laskemisesta löytyy tehtävien kuvauksesta. Tuloksia tulkitessa tulee huomioida, että arvioitavan oletetaan yrittävän parhaansa tehtäviä tehdessään.
Taulukko 1. Tehtäviäkokonaisuuksien nimet ja sisältö normitaulukoissa

Normiarvojen keskiarvot ja -hajonnat
Taulukossa 2 esitetään arvioitujen määrät sekä tehtäväkokonaisuuksien keskiarvot ja -hajonnat eri luokka-asteilla. Keskiarvot on pyöristetty kokonaisluvuiksi. Tulospalvelussa pylväskuviohin lisätyt punaiset normi-arvojen keskiarvoviivat perustuvat taulukon keskiarvoihin.
Taulukko 2. Arvioitujen määrät sekä ratkaisuprosenttien keskiarvot ja -hajonnat eri luokka-asteilla
Tulkintaohje
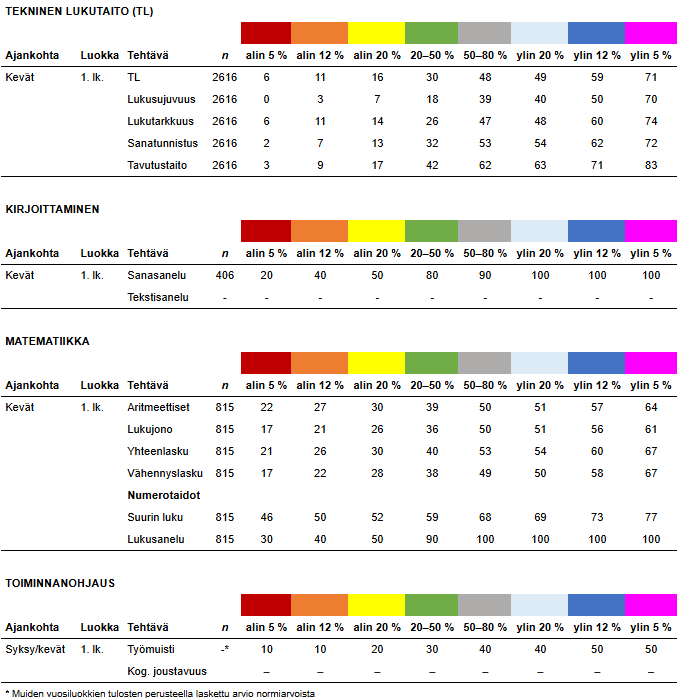
Tarkastellaan teknisen lukutaidon kokonaistulosta (TL). Mikäli oppilaan teknisen lukutaidon pylväs näkyy tulospalvelussa punaisena, tulos jää jakauman alimpaan viiteen prosenttiin suhteessa 2 616 keväällä testin teheeseen S1-oppimäärää opiskelevaan ekaluokkalaiseen. Alimmassa viidessä prosentissa teknisen lukutaidon keskimääräinen ratkaisuprosentti on maksimissaan kuusi prosenttia oikein.
Tarkastellaan aritmeettisten perustaitojen kokonaistulosta (Aritmeettiset). Mikäli oppilaan aritmeettisten perustaitojen pylväs näkyy tulospalvelussa sinisenä, tulos sijoittuu jakauman ylimpään 12 prosenttiin suhteessa 815 keväällä testin tehneeseen S1-oppimäärää opiskelevaan ekaluokkalaiseen. Ylimmässä 12 prosentissa arvioidun aritmeettisten perustaitojen keskimääräinen ratkaisuprosentti on 52–57 prosenttia oikein.
1. luokka kevät
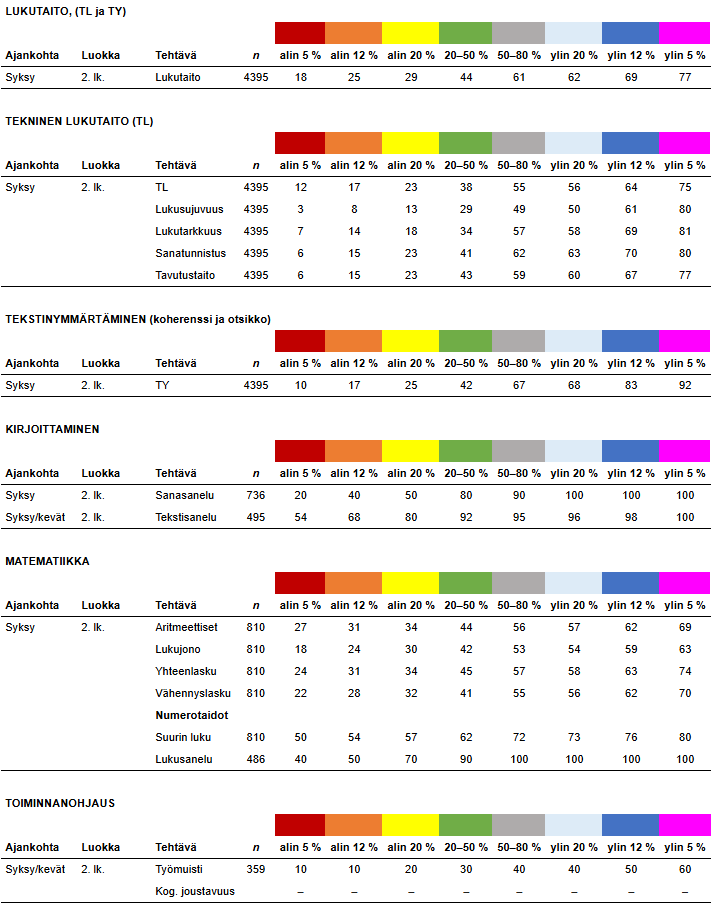
2. luokka syksy
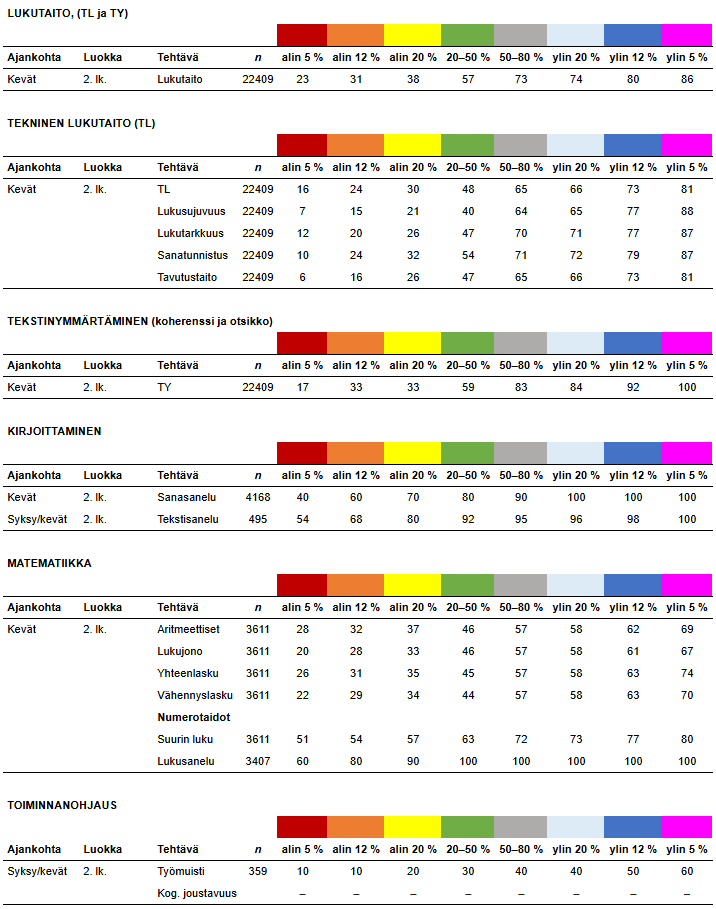
2. luokka kevät
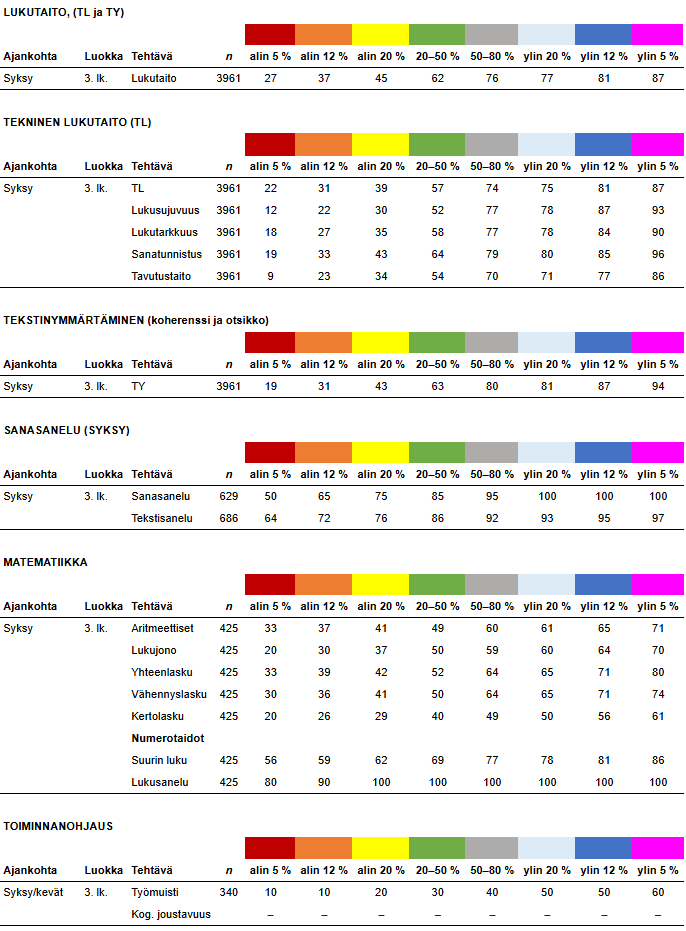
3. luokka syksy
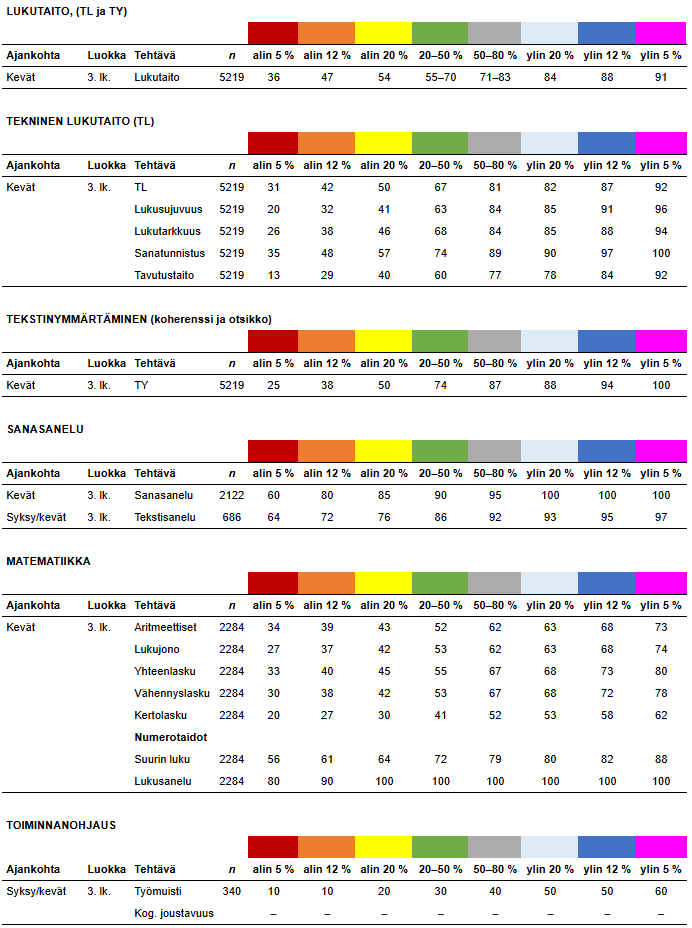
3. luokka kevät
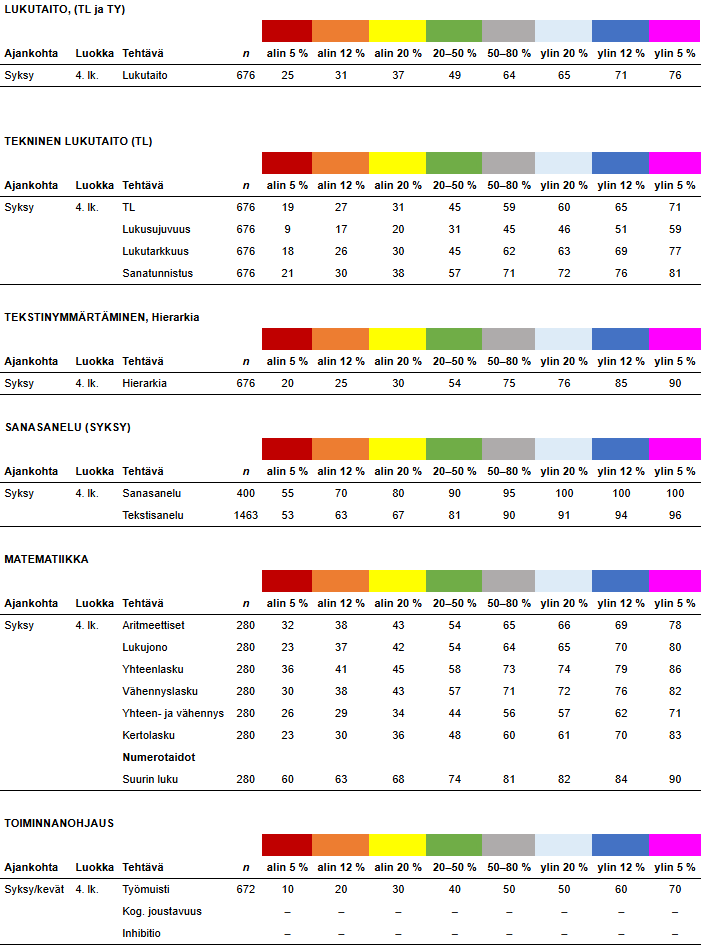
4. luokka syksy
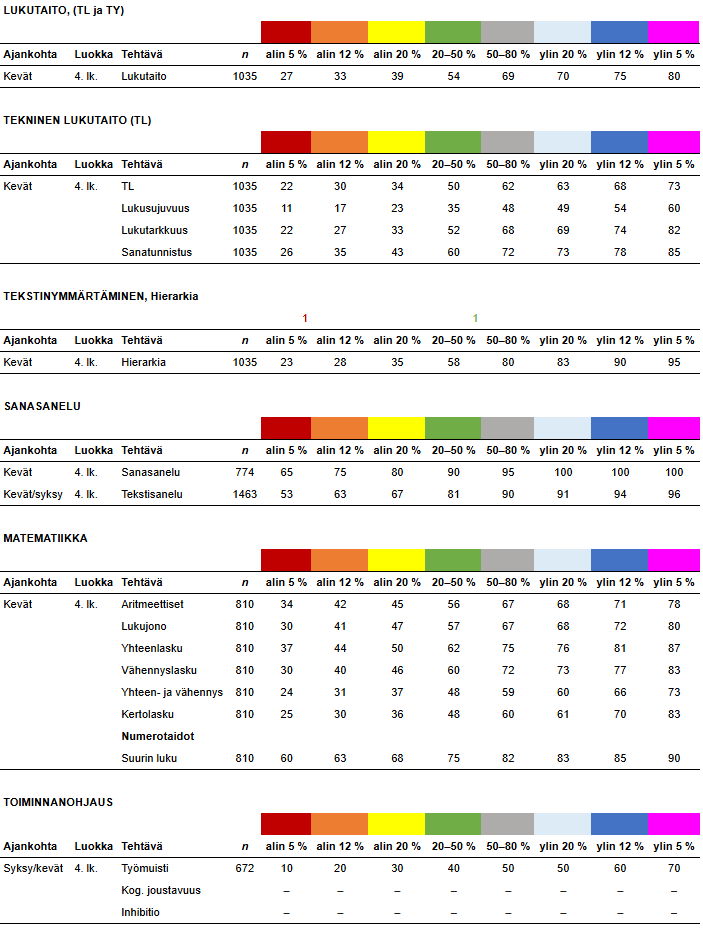
4. luokka kevät
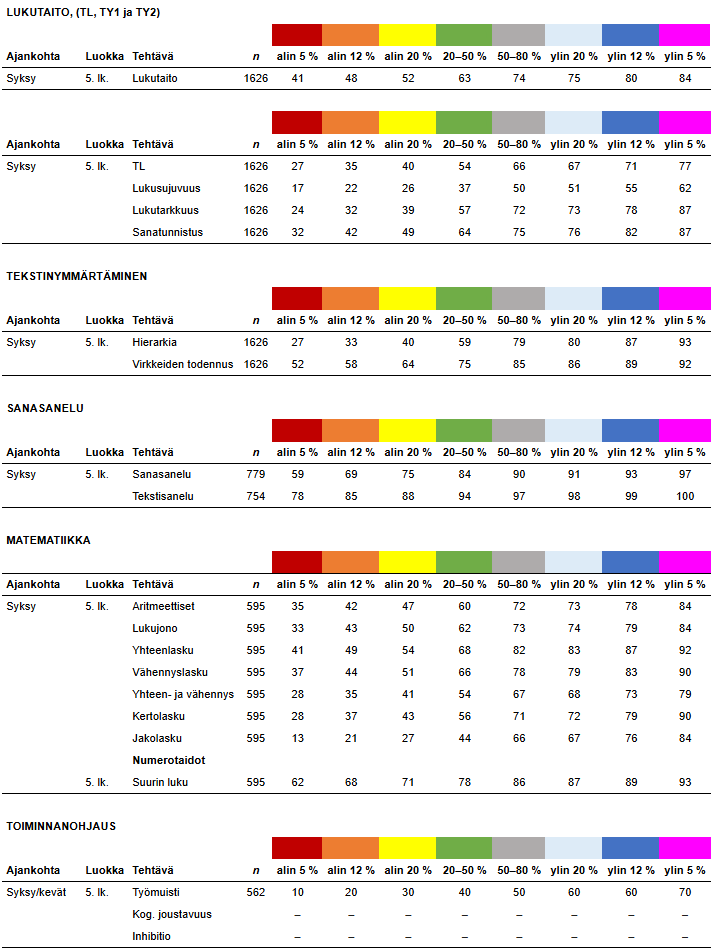
5. luokka syksy
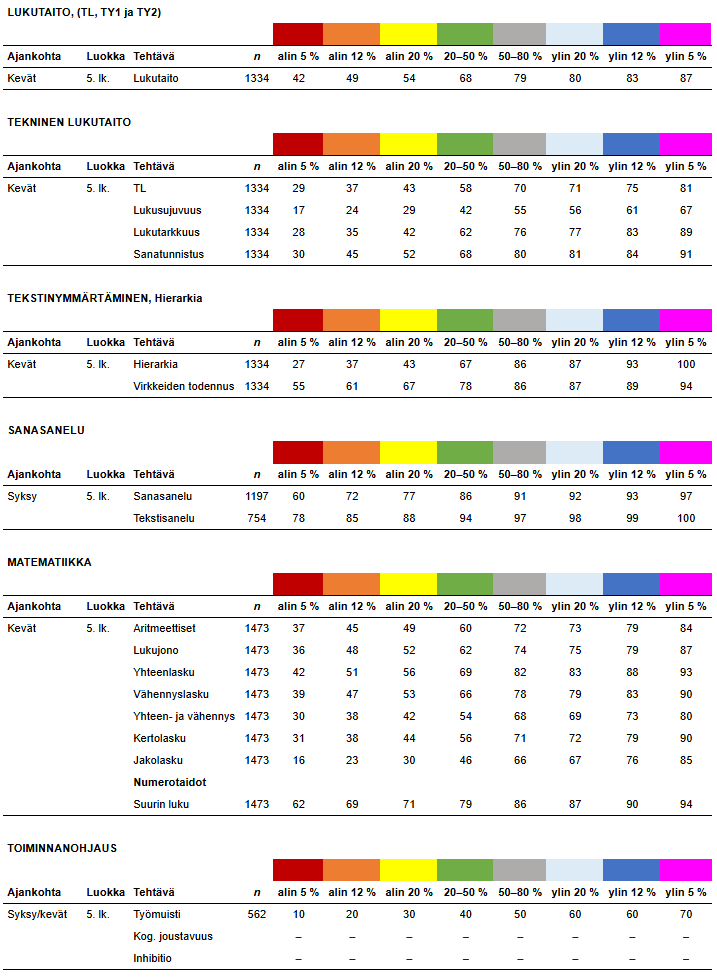
5. luokka kevät
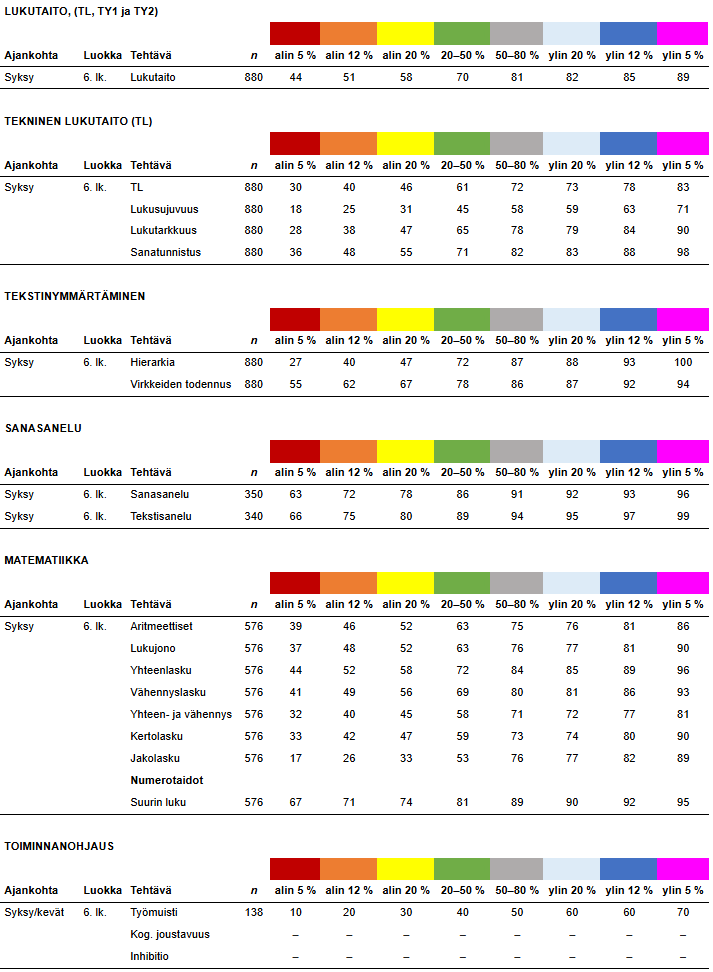
6. luokka syksy
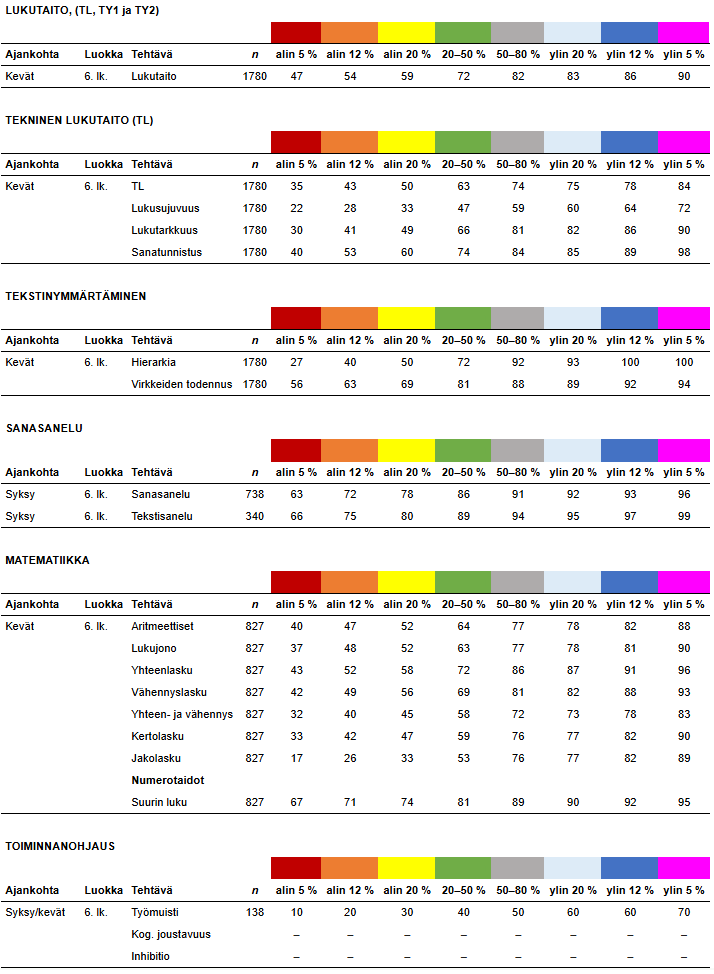
6. luokka kevät
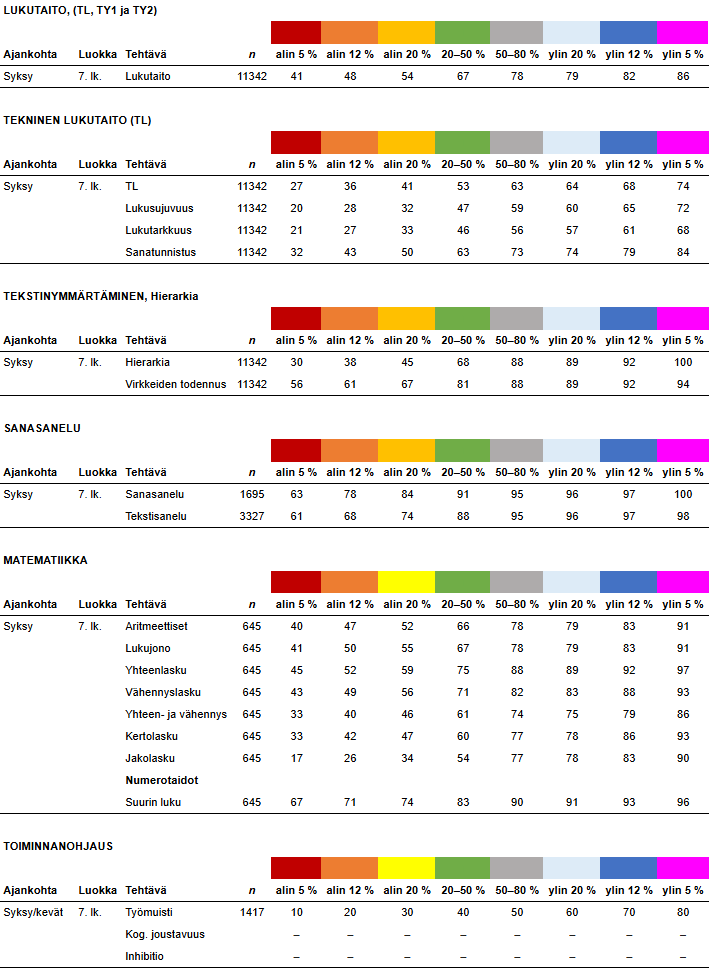
7. luokka syksy
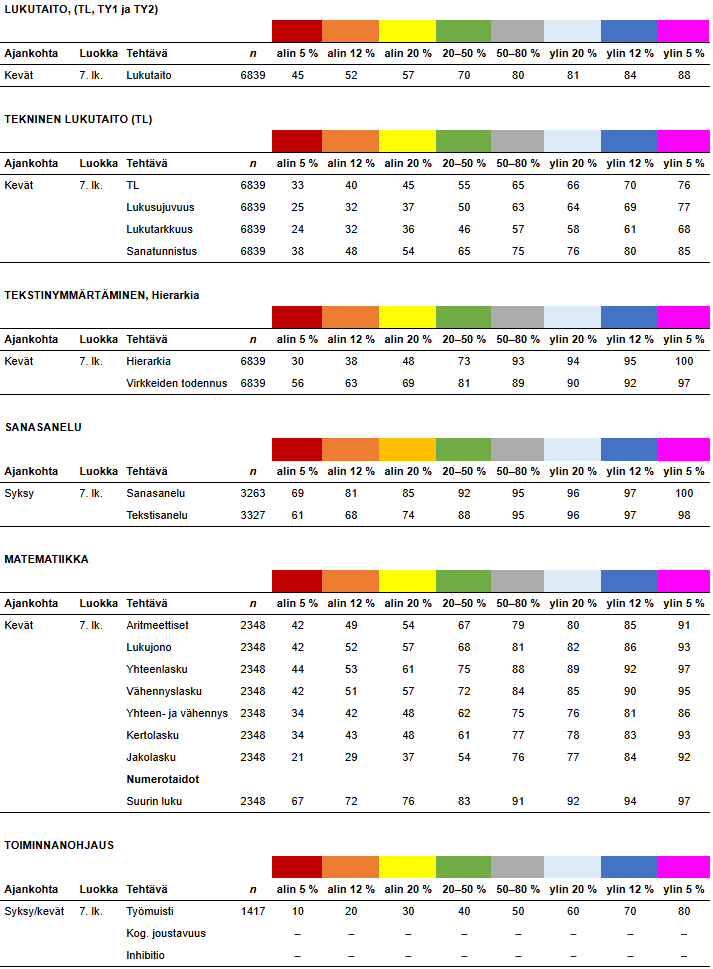
7. luokka kevät
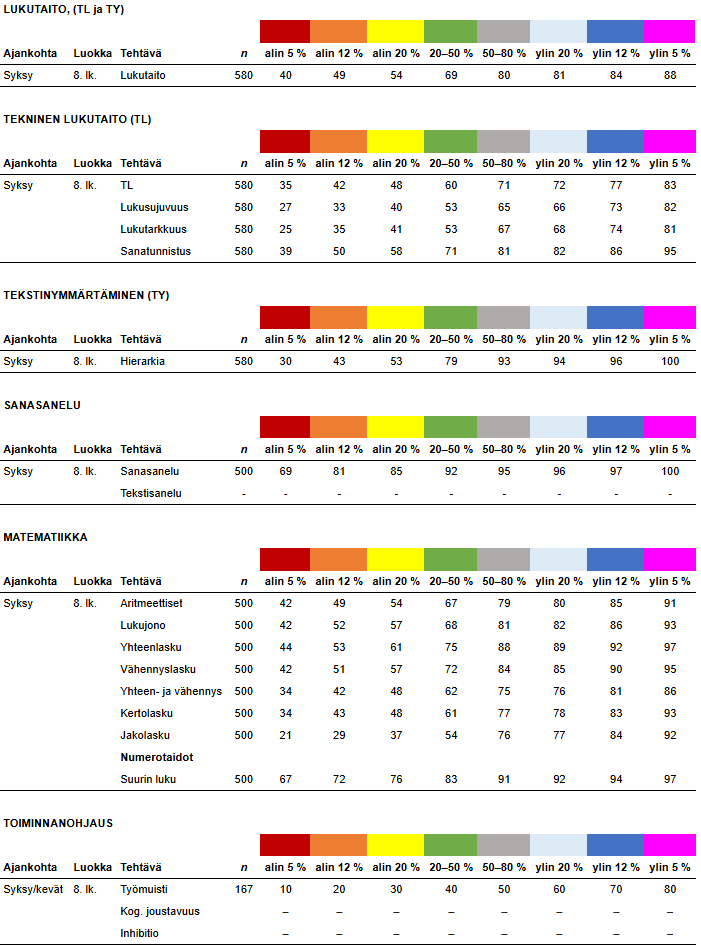
8. luokka syksy
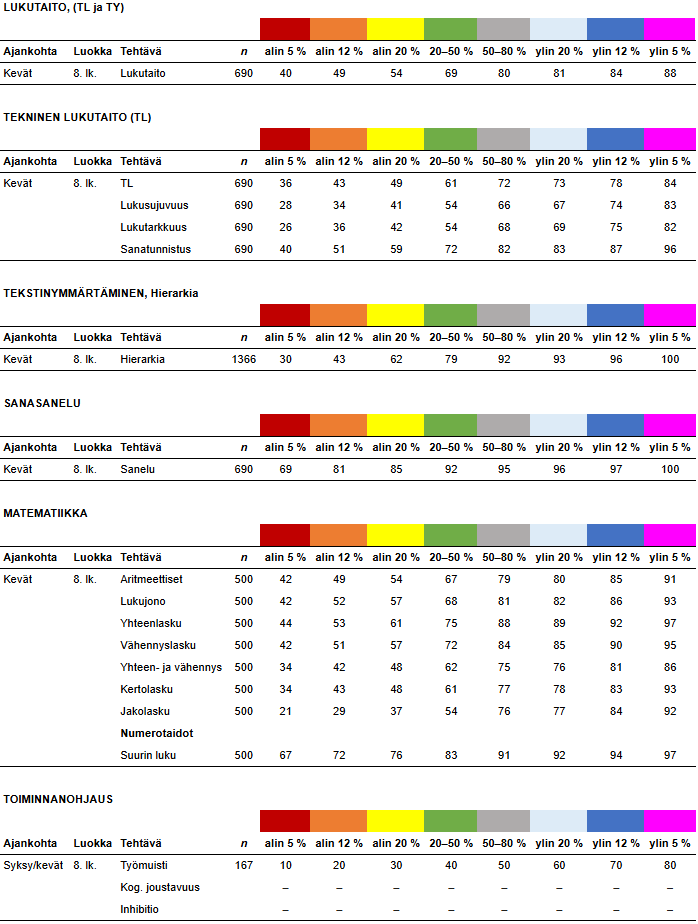
8. luokka kevät
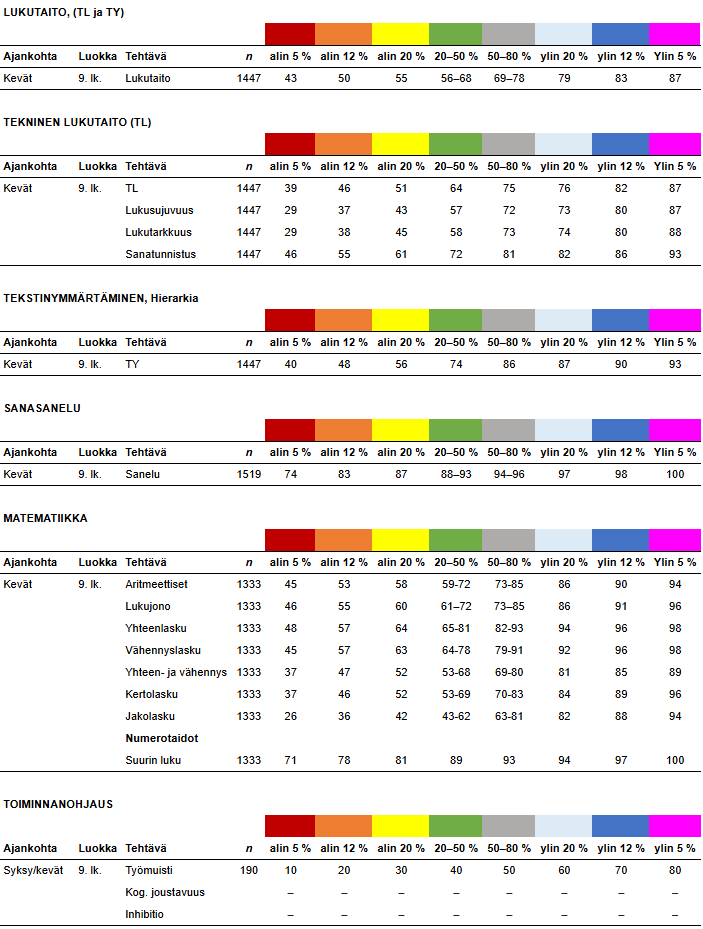
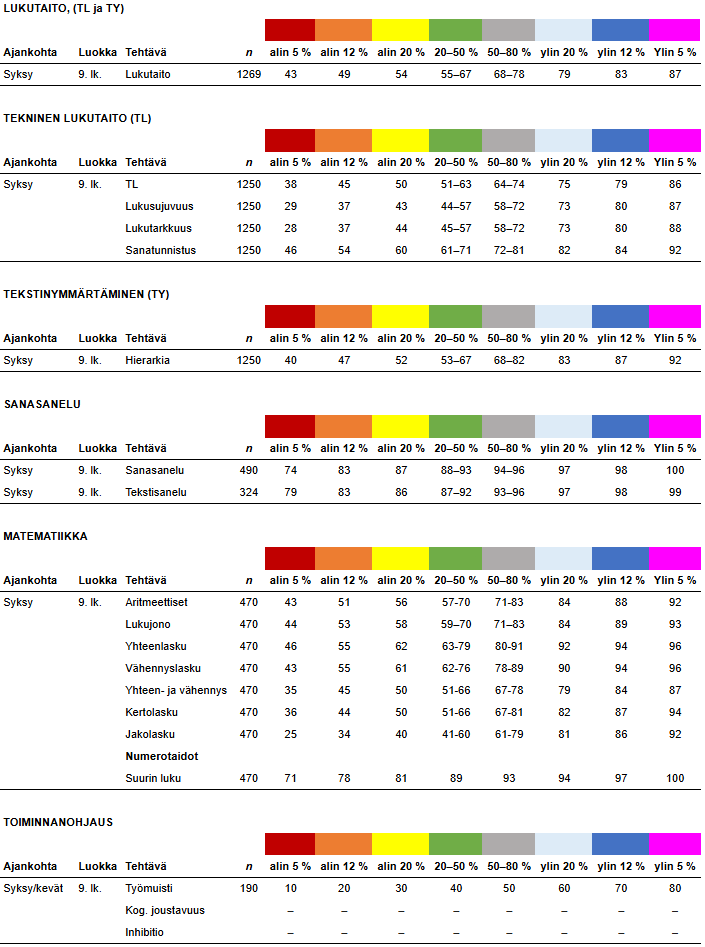
9. luokan kevään normit
Lukio, ammattikoulu, aikuisopiskelijat ja peruskoulun päätös